最高のコレクション 球 体積 公式 693986
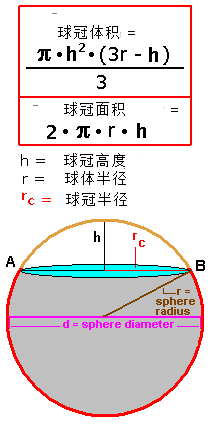
球冠在线计算器 在线计算 在线计算器 计算器在线计算
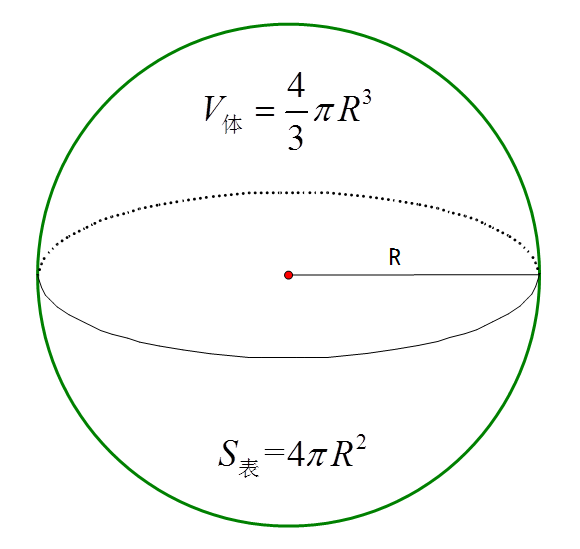
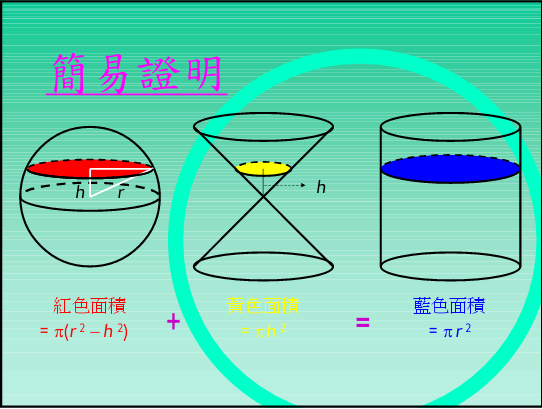
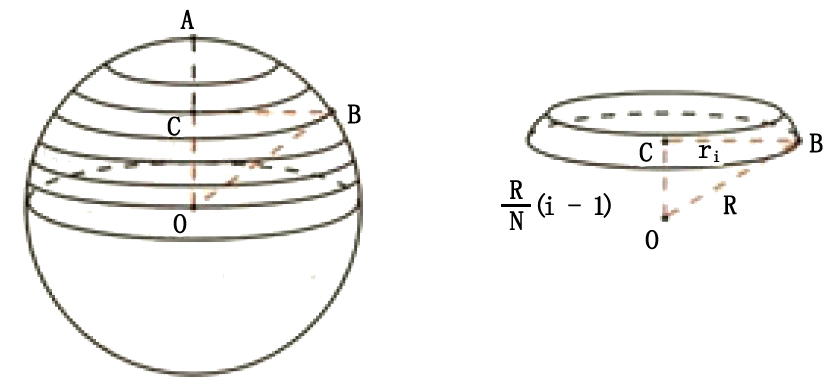
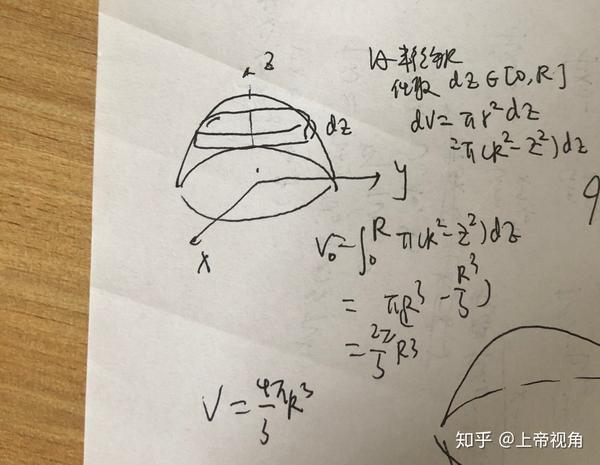
球の体積と表面積 半径 \(r\) の球の体積と表面積を求める公式は以下のようになります。 \(球の体積=\displaystyle \frac{4}{3}\pi r^3\) \(球の表面積=4\pi r^2\) 「なぜこの公式が成立するのか」については中学生の知識の範囲外です。 大学数学を使って球の体積を求めるシリーズ(目次)。 今回は3次元球の体積。結果は「球の体積の公式」になります。3次元球の体積3次元球 の体積を求めます。 「極座標のヤコビ行列とヤコビアン : 3次元」より、3次元極座標の体積要素は となるので(積分範囲も注意) まさしく「球の
球 体積 公式
球 体積 公式-球の体積 110 /80件 表示件数 5 10 30 50 100 0 1 1607 歳未満 / 小・中学生 / 非常に役に立った / 使用目的 関数グラフでオリンピックのロゴを作るときの計算に役立った 2 1306 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用の体積 V = 4 3πr3 V = 4 3 π r 3 体積 = 4 × 314 × 半径 × 半径 × 半径 ÷ 3 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 球の体積の求め方 」をご覧ください。 球の体積の求め方
1
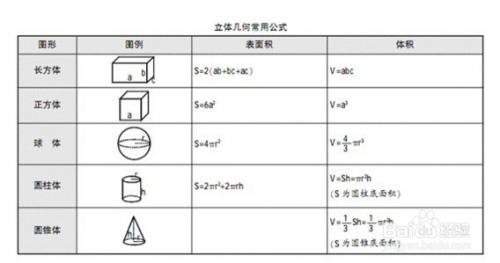
球の体積の公式を忘れちゃったときに参考にしてみて。 球の体積の公式を1発で覚える方法 「球の体積の公式」を暗記する方法を伝授しよう。 3分の4 × 円周率 × 半径の三乗 という公式はつぎの語呂を使えばおぼえられちゃうよ。球 球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよいだけです。 このページの続きでは、例題を使って、この 半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求め
高次元の球とその体積とは n n n 次元(ユークリッド)空間において, x 1 2 x 2 2 ⋯ x n 2 ≤ R 2 x_1^2x_2^2\cdots x_n^2\leq R^2 x 1 2 x 2 2 ⋯ x n 2 ≤ R 2 を満たす点の集合を半径 R R R の n n n 次元球と言います。特に R = 1 R=1 R = 1 のとき,単位球と言います。 エクセルで球の体積を計算する方法 同様の手順でエクセルの半径から球の体積に換算する方法について確認していきましょう。 まず、球の体積の定義は体積=4/3 πr^3 となります。 表面積を算出したときと同様に、球の体積も同時に計算していきましょう。 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4πr2 →「心配アール二乗」 球の体積: 4 3 π r 3
球 体積 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | 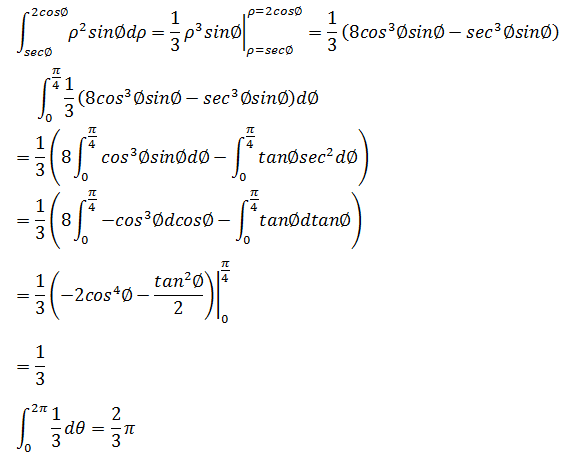 |  |
 |  | |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
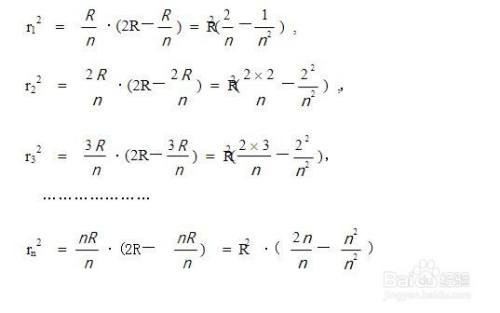 |  | |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 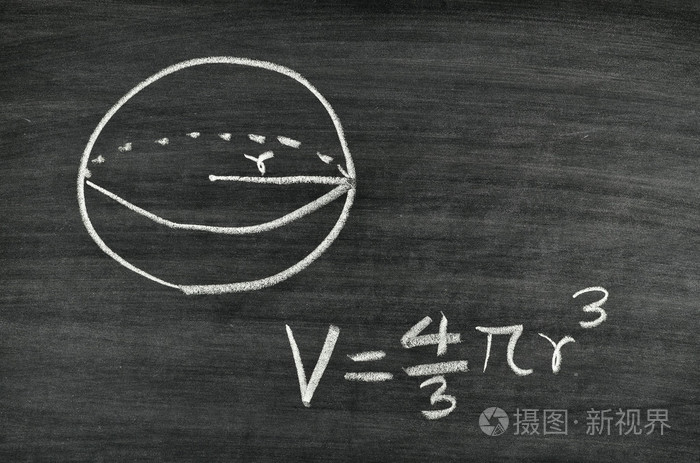 |  |
 | ||
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 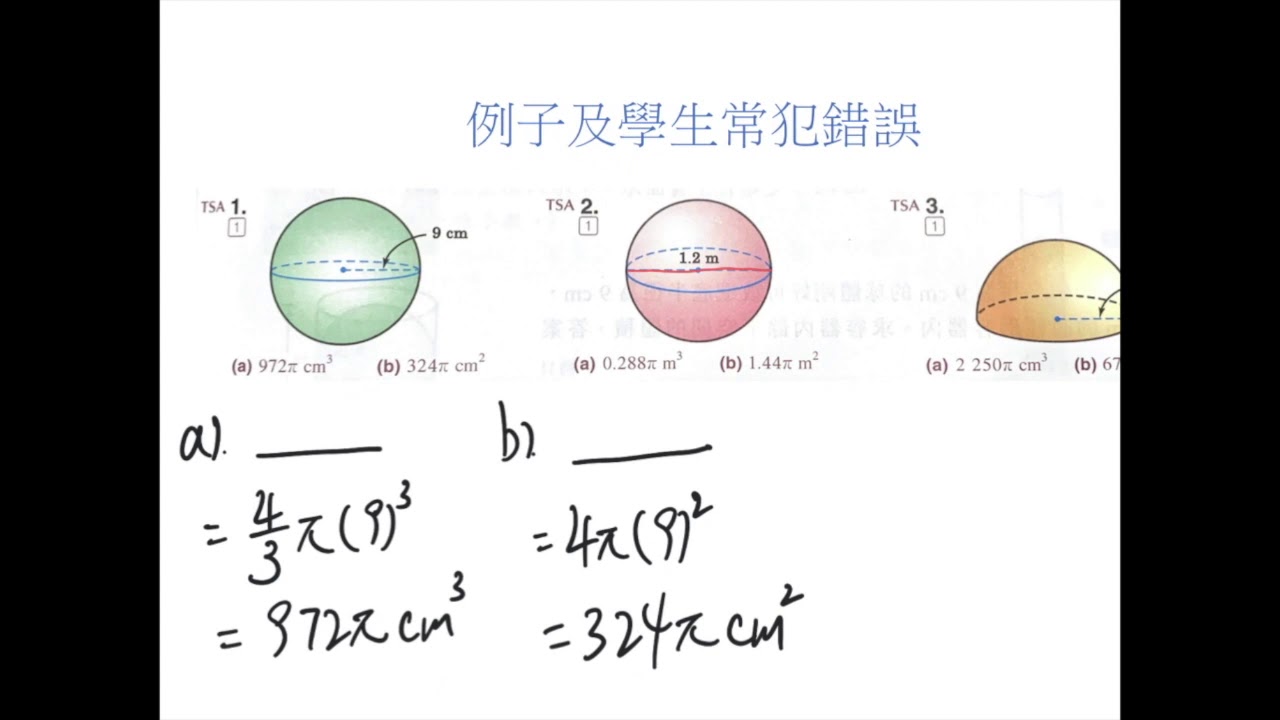 |  |
 |  | |
「球 体積 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
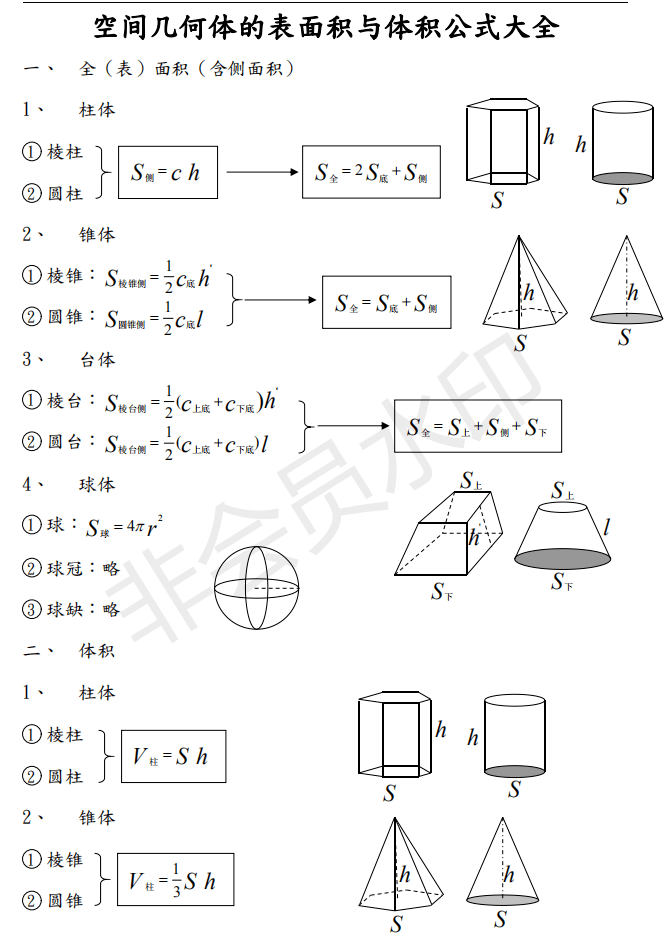 |
球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半
コメント
コメントを投稿